期權的風險與對沖
期權的「厚尾風險(Fat Tail Risk)」,亦稱「極端風險」或「黑天鵝風險」,意指當標的資產於極短時間內出現劇烈價格波動(如暴漲或暴跌)時,期權組合將面臨巨大、非線性且無法預測的損失風險。
什麼是尾部風險(Tail Risk)
在金融統計領域,資產報酬分布通常並非完美常態分布,而傾向出現「厚尾」現象,這代表極端事件雖然發生機率低,但一旦發生,影響顯著且損失重大。
對選擇權交易者而言:
- 賣方策略(例如裸賣 Put、Iron Condor、Strangle 等)雖然勝算高,但若遇到尾部事件,可能導致災難性虧損。
- 買方策略(例如 Long Put、Straddle)則有機會藉由尾部風險進行避險或獲利。
範例說明:
假設某投資人賣出 1 份 BTC 的 $80,000 Put(收取權利金 $1,000),當時現價為 $100,000,並認為 BTC 不至於短期內暴跌。
但若市場急速崩盤:
- BTC 在數天內跌至 $60,000。
- 需以 $80,000 買入 1 枚 BTC,當時現價僅 $60,000。
- 損失 = $20,000 − $1,000 = $19,000
原本預期僅獲利 $1,000,但實際損失將近 20 倍,這即為典型的「尾部風險」情境。
尾部風險的表現型態:
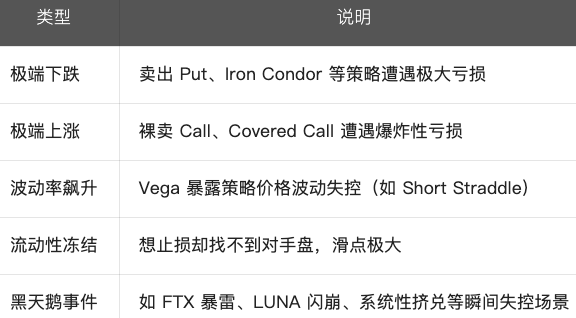
如何應對及管理尾部風險?
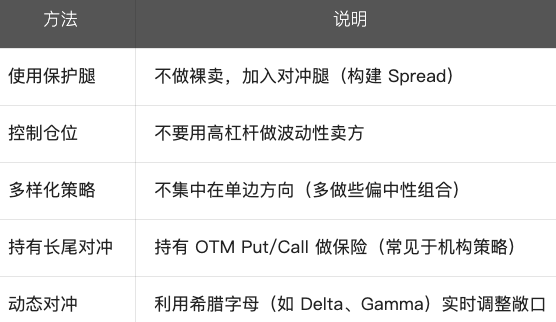
結論:
尾部風險是選擇權策略中極具破壞性的潛在重大風險,對賣方策略尤為關鍵。建議勿僅因「勝算高」而忽略風險曝險。穩健的選擇權交易,應以在極端情境下仍能維持運作的策略架構為主。
什麼是 Whalley-Wilmott 漸進最適避險模型(Asymptotic Optimal Hedging)
Whalley-Wilmott 模型由 Paul Wilmott 與 Anne Whalley 提出,是一套專為動態避險(Dynamic Hedging)設計的方法,主要目的是在存在交易成本(Transaction Costs)前提下,將避險成本風險最小化。此模型屬於漸進最適(Asymptotically Optimal)避險策略,適合用於高頻調整的避險組合。
核心理念
在 Black-Scholes 模型中,理論上選擇權賣方可藉由連續調整(Continuous Delta Hedging)完全對沖風險。然而,現實情境下:
- 交易成本(手續費、市場買賣價差)使得頻繁調整部位的成本非常高。
- 離散避險(Discrete Hedging)則無法徹底消除風險。
Whalley-Wilmott 模型的目標為:
在交易成本與風險之間取得最佳平衡,也就是說避險次數不宜過高(以免成本過重),亦不可過低(避免風險曝險過大)。
關鍵公式
Whalley-Wilmott 提出最適避險區間(不交易區間,No-Trade Region),僅當標的資產價格超出該區間時才進行調整:
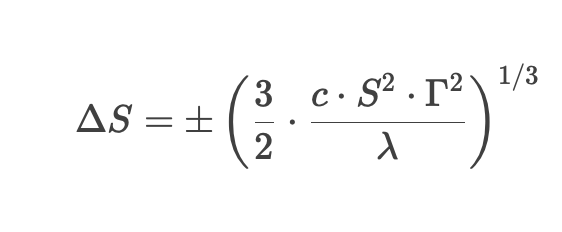
其中:
- ΔS = 觸發避險的價格變動門檻
- c = 交易成本(比例)
- S = 標的資產價格
- Γ = 選擇權 Gamma(二階導數)
- λ = 風險厭惡係數(Risk Aversion)
策略規則:
1. 計算現有選擇權的 Delta(對沖比例)。
2. 設定一個不交易區間(No-Trade Region),只要資產價格位於區間內,則無需進行避險調整。
3. 當價格超出該區間時,立即調整部位,讓 Delta 回復至目標水準。
4. 特點說明
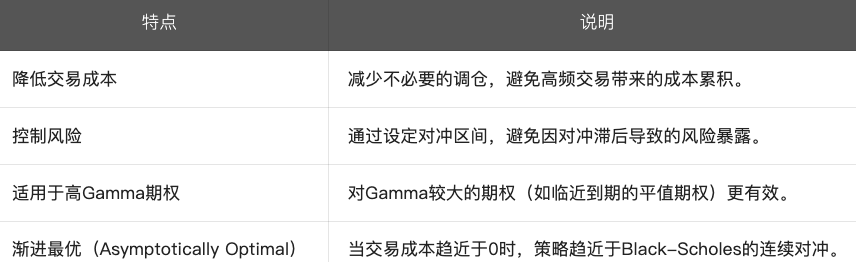
5. 與其他避險方式比較

6. 結論
- Whalley-Wilmott 模型是一種納入交易成本考量的動態避險優化工具。
- 透過「不交易區間」(No-Trade Region)設計,減少不必要調整,並有效控管風險。
- 特別適合高 Gamma 選擇權或高交易成本環境,是 Black-Scholes 模型的實務改良版。
此模型廣泛應用於量化選擇權交易與風險控管領域。尤其適合需權衡交易成本與風險曝險的機構投資人。





