Risco e Proteção de Opções

O que é o Risco de Cauda

Na estatística financeira, as distribuições de retorno dos ativos costumam desviar do padrão normal perfeito. Nesses casos, apresentam “distribuições de cauda grossa”, em que eventos extremos são estatisticamente improváveis, mas causam impactos imensos e têm poder destrutivo significativo quando acontecem.

Para quem opera opções:

• Estratégias de venda (como venda nua de Puts, Iron Condors e Strangles) oferecem altas taxas de sucesso, mas estão sujeitas a perdas devastadoras em eventos de cauda
• Estratégias de compra (como Long Puts ou Straddles) podem proteger contra o risco de cauda ou até lucrar com ele

Exemplo:

Imagine que você vendeu uma Put de BTC a US$ 80.000 (prêmio recebido: US$ 1.000), enquanto o preço do ativo estava em US$ 100.000. Você aposta que o BTC não cairá tão rapidamente.

Porém, se o mercado despenca:

• O BTC cai para US$ 60.000 em questão de dias
• Você é obrigado a comprar um BTC por US$ 80.000 quando o mercado paga apenas US$ 60.000
• Prejuízo = US$ 20.000 - US$ 1.000 = US$ 19.000

O prêmio aparentemente pequeno (US$ 1.000) se transforma em um prejuízo massivo, quase 20 vezes maior — um clássico caso de explosão de “risco de cauda”.

Formas de Risco de Cauda:

Como Lidar e Gerenciar o Risco de Cauda:

Conclusão:

O risco de cauda é uma ameaça silenciosa e extremamente destrutiva em estratégias com opções, especialmente para vendedores. Não é possível ignorar a exposição ao risco apenas por “altas taxas de acerto”. Para operar opções de forma realmente robusta, é fundamental adotar uma estratégia capaz de resistir mesmo diante de condições extremas de mercado.

O que é o Modelo Assimptoticamente Ótimo de Hedge de Whalley-Wilmott?

O modelo Whalley-Wilmott, criado por Paul Wilmott e Anne Whalley, é um método de hedge dinâmico que visa principalmente minimizar os riscos de custos na proteção, especialmente quando existem custos transacionais. Essa abordagem é considerada uma estratégia assimptoticamente ótima de hedge, indicada para portfólios que demandam ajustes frequentes de proteção.

Conceito Fundamental

No modelo Black-Scholes, em teoria, quem vende opções conseguiria se proteger totalmente contra os riscos fazendo ajustes contínuos (Delta Hedging Contínuo). Na prática, porém:

• Os custos de transação (taxas, spread entre compra e venda) tornam o rebalanceamento frequente caro
• O hedge feito de forma discreta não elimina completamente a exposição ao risco

Objetivo do Modelo Whalley-Wilmott:

Encontrar o equilíbrio ideal entre custos de transação e riscos — ou seja, proteger-se sem rebalancear demais (evitando custos excessivos), nem de menos (evitando exposição indesejada).

Fórmula Principal

O modelo Whalley-Wilmott determina um intervalo ótimo para hedge (“Região de Não-Negociação”) — só é feito ajuste quando o preço do ativo subjacente sai desse intervalo:

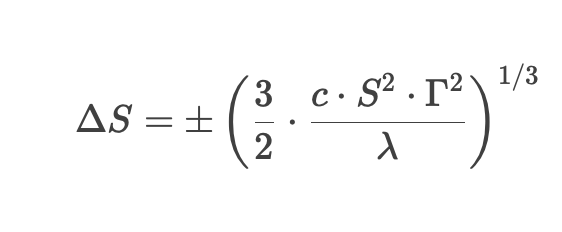
Nessa fórmula:

• Δ S = limite de variação de preço que aciona o hedge
• c = custo de transação (proporcional)
• S = preço do ativo subjacente
• Γ = Gama da opção (sensibilidade de segunda ordem)
• λ = coeficiente de aversão ao risco

Regras da Estratégia:

1.Calcular o Delta vigente da opção (índice de hedge)
2.Definir um intervalo de tolerância (“Região de Não-Negociação”) — enquanto o preço do ativo permanecer nesse intervalo, não há ajuste
3.Se o preço ultrapassar o intervalo, ajustar a posição para restaurar o Delta ao nível desejado
4.Principais características

5.Comparação com Outros Métodos de Hedge:

6.Resumo

• O modelo Whalley-Wilmott é um método de otimização dinâmica de hedge que leva em conta os custos de transação
• Reduz rebalanceamentos desnecessários enquanto controla riscos ao definir zonas de não-ajuste (“no-trade region”)
• Recomendado para opções com alto Gama ou em contextos de custos transacionais elevados, sendo uma evolução prática do modelo Black-Scholes

Esse modelo tem aplicações essenciais em trading quantitativo de opções e gestão de riscos, e é especialmente útil para investidores institucionais que precisam equilibrar custos transacionais e exposição ao risco.