Risikomanagement und Absicherungsstrategien bei Optionen

Was versteht man unter Tail Risk?

In der Finanzstatistik weichen die Renditeverteilungen von Vermögenswerten häufig deutlich von einer idealen Normalverteilung ab. Stattdessen treten sogenannte „fett-schwänzige Verteilungen“ auf, in denen Extremereignisse zwar statistisch selten, aber bei ihrem Eintritt erhebliche Auswirkungen und enorme Zerstörungskraft haben können.

Für Optionshändler gilt:

• Verkäuferstrategien (zum Beispiel ungedeckte Short Puts, Iron Condors oder Strangles) erzielen häufig eine hohe Gewinnquote, führen bei Tail Events jedoch oft zu katastrophalen Verlusten
• Käuferstrategien (wie Long Puts oder Straddles) bieten hingegen die Möglichkeit, Tail Risk abzusichern oder davon zu profitieren

Beispiel:

Nehmen wir an, Sie verkaufen einen BTC $80.000 Put (Prämie: $1.000), während der aktuelle Kurs bei $100.000 liegt. Sie gehen davon aus, dass Bitcoin nicht innerhalb kürzester Zeit stark fällt.

Kommt es jedoch zu einem starken Kursrückgang:

• BTC fällt innerhalb weniger Tage auf $60.000
• Sie sind verpflichtet, einen Bitcoin zum Preis von $80.000 zu kaufen, während der Marktpreis nur $60.000 beträgt
• Verlust: $20.000 abzüglich $1.000 = $19.000

Die ursprünglich erwartete kleine Prämie ($1.000) verwandelt sich in einen massiven Verlust, der fast das 20-fache beträgt – das ist ein typischer „Tail Risk“-Fall.

Formen von Tail Risk:

Wie lässt sich Tail Risk adressieren und steuern?

Fazit:

Tail Risk ist eine äußerst zerstörerische, oft unterschätzte Gefahr in Optionsstrategien und für Verkäufer besonders riskant. Ein hohes Gewinnverhältnis darf nicht darüber hinwegtäuschen, dass das Risiko stets im Blick behalten werden muss. Nachhaltig erfolgreiche Optionsstrategien basieren auf einem System, das auch unter Extrembedingungen am Markt bestehen kann.

Was ist das Whalley-Wilmott Asymptotic Optimal Hedging Model?

Das Whalley-Wilmott-Modell, entwickelt von Paul Wilmott und Anne Whalley, ist ein dynamisches Hedging-Verfahren, das gezielt das Kostenrisiko beim Absichern einer Position minimiert – insbesondere, wenn Transaktionskosten bestehen. Es gilt als asymptotisch optimales Hedging-Modell und eignet sich besonders für Portfolios, die häufige Hedging-Anpassungen erfordern.

Kernkonzept

Im idealtypischen Black-Scholes-Modell können Optionsverkäufer ihr Risiko durch kontinuierliches Delta-Hedging vollständig ausgleichen. Doch in der Praxis gilt:

• Transaktionskosten (wie Gebühren oder Spreads) machen häufige Hedging-Anpassungen teuer
• Risiko wird durch diskretes Hedging nie ganz eliminiert

Ziel des Whalley-Wilmott-Modells:

Das optimale Verhältnis zwischen Transaktionskosten und Risikobegrenzung zu finden – die Hedging-Frequenz darf weder zu hoch (zu teuer) noch zu niedrig (zu riskant) sein.

Schlüsselformel

Das Whalley-Wilmott-Modell definiert ein optimales Hedging-Intervall („No-Trade Region“ (Nicht-Handels-Intervall)): Anpassungen erfolgen nur, wenn der Preis des Basiswerts dieses Intervall verlässt:

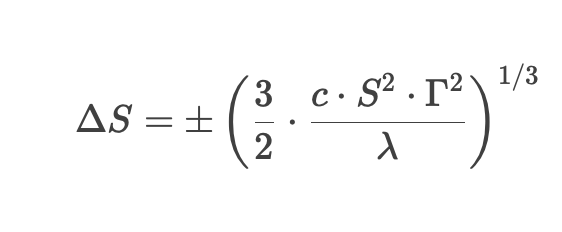
Die Formel beinhaltet:

• Δ S = Preisschwelle, bei deren Überschreitung ein Hedging ausgelöst wird
• c = Transaktionskostenanteil
• S = Preis des Basiswerts
• Γ = Gamma der Option (Sensitivität zweiter Ordnung)
• λ = Risikoaversionkoeffizient

Strategieregeln:

1. Aktuelles Delta der Option (Delta-Quote) berechnen
2. Toleranzspanne („No-Trade Region“) festlegen – solange der Preis im Intervall bleibt, nicht hedgen
3. Bei Überschreiten des Intervalls Position anpassen, damit das Delta wieder dem Ziel-Delta entspricht
4. Eigenschaften

5. Vergleich zu anderen Hedging-Methoden:

6. Zusammenfassung

• Das Whalley-Wilmott-Modell ist eine dynamische Optimierungsmethode für Hedging-Strategien, die Transaktionskosten explizit berücksichtigt
• Durch die Definition von „No-Trade Regions“ werden unnötige Umschichtungen vermieden und das Risiko effizient kontrolliert
• Das Modell eignet sich besonders für Optionen mit hohem Gamma oder in Märkten mit hohen Transaktionskosten und stellt eine praxisnahe Weiterentwicklung zum Black-Scholes-Modell dar

Gerade in der quantitativen Optionsstrategie und im Risikomanagement, insbesondere für institutionelle Investoren, die ein Gleichgewicht zwischen Transaktionskosten und Risiko anstreben, spielt dieses Modell eine besondere Rolle.