Volatilitätsarbitrage-Strategien

Straddle-Strategie

Definition:

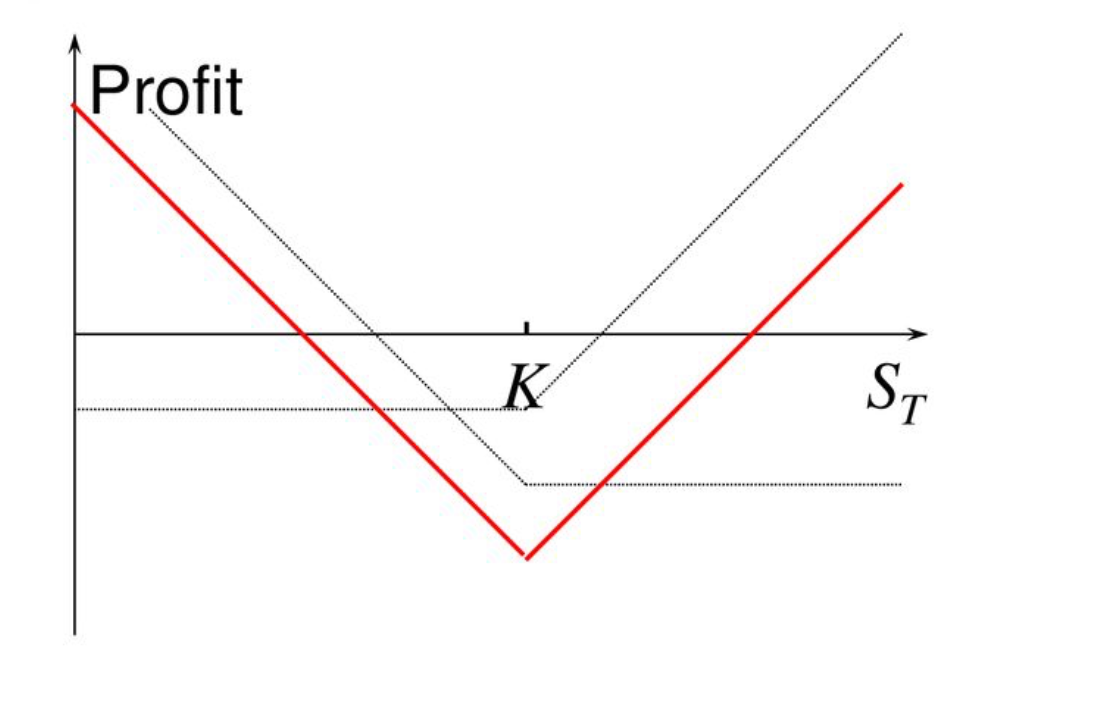
• Bei der Straddle-Strategie werden gleichzeitig eine Call-Option und eine Put-Option auf denselben Basiswert mit identischem Ausübungspreis und Verfallsdatum erworben.
• Ziel ist es, von markanten Kursbewegungen des Basiswerts in beide Richtungen (aufwärts oder abwärts) zu profitieren.

Strategie-Überblick:

Zweistufige Gewinnchance: Bewegt sich der Kurs stark nach oben oder unten, erzielt eine Option genügend Gewinn, um den Verlust der anderen zu decken.

Hohes Risiko: Nur bei ausreichend starker Kursbewegung können die Optionsprämien ausgeglichen werden. Bei geringen Schwankungen verfallen die Optionen wertlos, was zu deutlichen Verlusten führt.

Hohe Kosten: Da beide Optionen gleichzeitig gekauft werden, sind die anfänglichen Kosten (Prämien) für Straddles meist hoch.

Anwendungsbeispiel der Straddle-Strategie

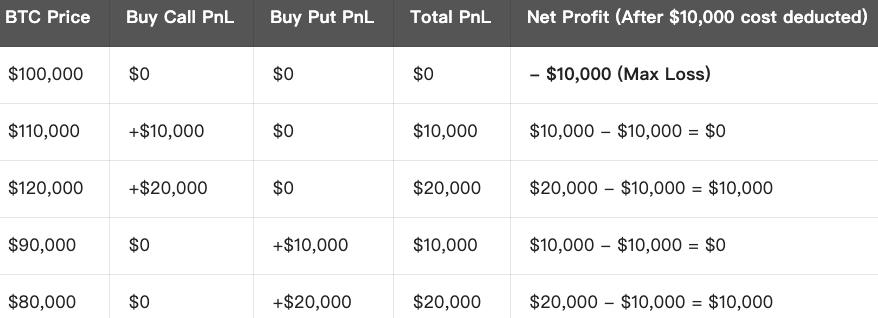
Angenommen, der BTC-Kurs liegt aktuell bei $100,000. Sie rechnen mit hoher Volatilität, wissen aber nicht, ob der Kurs steigen oder fallen wird. Daher setzen Sie eine Straddle-Strategie ein:

Nettokosten:

• Gesamtkosten = $5,000 (Call-Prämie) + $5,000 (Put-Prämie) = $10,000

Ergebnis bei Fälligkeit:

Strategie-Überblick:

Maximalverlust: Bleibt der Kurs unverändert oder reicht die Volatilität nicht aus, entspricht der Maximalverlust der gezahlten Gesamtprämie ($10,000).

Maximalgewinn: Es besteht nach oben keine Begrenzung – je stärker die Kursbewegung, desto höher der Gewinn.

Break-Even-Punkte: Die Kursbewegung muss die gezahlte Prämie überschreiten, also **$100,000 + $10,000 = $110,000** bzw. $100,000 - $10,000 = $90,000.

Anwendungsszenario:

• Straddle-Strategien eignen sich besonders bei zu erwartender hoher Volatilität, aber unklarer Marktrichtung – etwa vor der Veröffentlichung wichtiger Finanzdaten, politischer Bekanntgaben oder bedeutender Ereignisse.

Fazit:

Die Straddle-Strategie eignet sich, wenn sowohl Kursanstiege als auch -rückgänge möglich sind. Sie profitiert von erheblicher Volatilität des Basiswerts, erfordert aber ausreichend starke Schwankungen, um die Optionskosten zu decken.

Strangle-Strategie

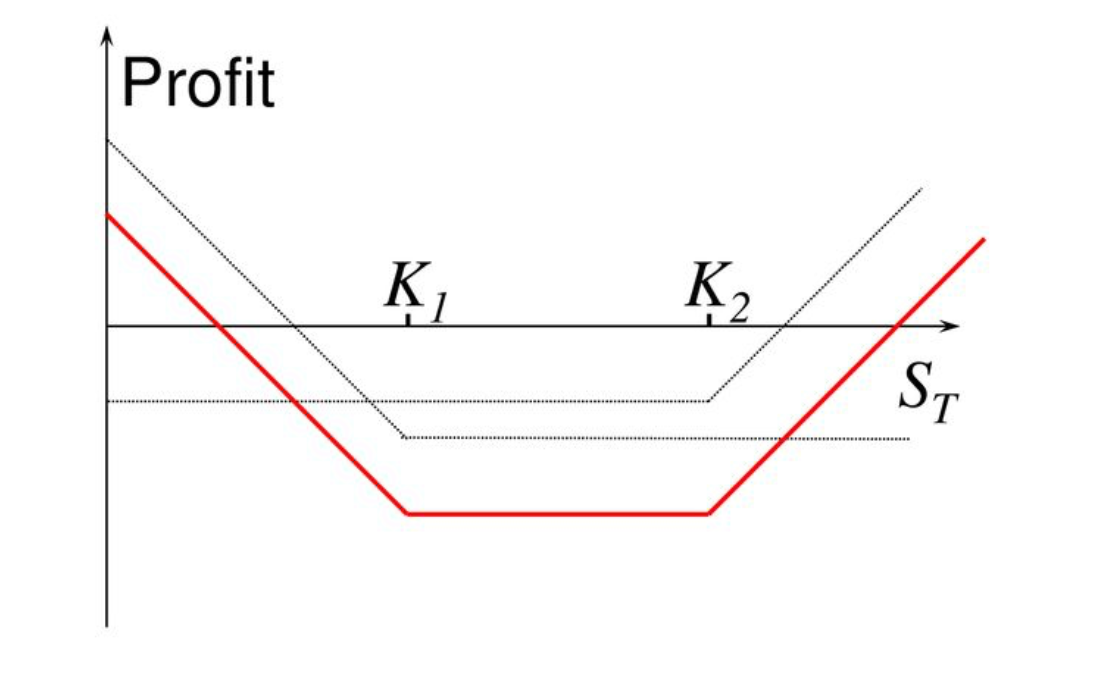
• Die Strangle-Strategie ist ideal, wenn starke Kursschwankungen erwartet werden, die Richtung jedoch ungewiss ist. Sie ähnelt der Straddle, verwendet aber verschiedene Ausübungspreise und ist dadurch oft günstiger.
• Das Hauptziel: von starken Preisbewegungen zu profitieren – unabhängig von der Richtung.

Abgrenzung zur Straddle:

• Straddle: Kauf von Call- und Put-Optionen zum gleichen Ausübungspreis.
• Strangle: Kauf von Call- und Put-Optionen zu unterschiedlichen Ausübungspreisen, wodurch der Prämienaufwand sinkt.

Anwendungsbeispiel der Strangle-Strategie

Angenommen, der aktuelle BTC-Kurs liegt bei $100,000. Sie rechnen mit deutlicher Volatilität, wissen aber nicht, ob sich der Kurs nach oben oder unten bewegt – also setzen Sie die Strangle-Strategie ein:

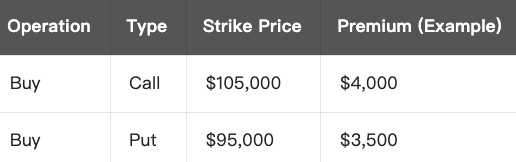
Gesamtkosten:

• Gesamtkosten = $4,000 (Call-Prämie) + $3,500 (Put-Prämie) = $7,500

Ergebnis bei Fälligkeit:

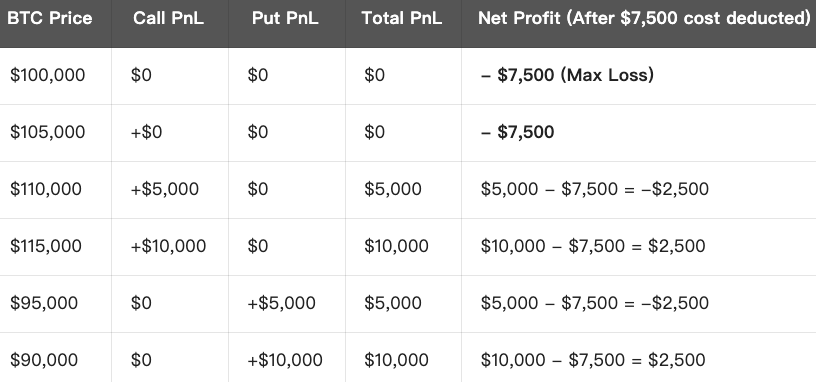
Strategie-Überblick:

Maximalverlust: Bleibt der Marktpreis zwischen den beiden Ausübungspreisen, entspricht der Verlust der gezahlten Gesamtprämie ($7,500).

Maximalgewinn: Eine Obergrenze gibt es nicht – je stärker die Kursschwankung, desto größer der Gewinn in beiden Richtungen.

Break-Even-Punkte: Die Preisbewegung muss die Gesamtkosten der Optionen übersteigen:

• Oberer Break-Even = Ausübungspreis (Call) + Gesamtprämie = $105,000 + $7,500 = $112,500
• Unterer Break-Even = Ausübungspreis (Put) - Gesamtprämie = $95,000 - $7,500 = $87,500

Anwendungsszenario:

• Die Strangle-Strategie empfiehlt sich bei hoher erwarteter Volatilität, wenn die Richtung des Kursschlags unklar ist.
• Typische Anwendungsfälle: bevorstehende Wirtschaftsdaten, regulatorische Ankündigungen oder zentrale Marktereignisse.
• Der größte Vorteil gegenüber der Straddle-Strategie sind geringere Prämien und ein reduziertes Risiko, allerdings sind für Gewinn größere Kursbewegungen notwendig.

Fazit:

Mit der Strangle-Strategie lässt sich durch den günstigen Erwerb von Calls und Puts zu verschiedenen Ausübungspreisen bei starker Marktvolatilität risikoarm profitieren.

Short-Strangle-Strategie

Definition:

• Bei der Short-Strangle-Strategie verkauft man eine Call- und eine Put-Option auf den gleichen Basiswert mit unterschiedlichen Ausübungspreisen und identischem Fälligkeitsdatum.
• Diese Strategie eignet sich, wenn geringe Volatilität und ein stabiler Preisverlauf erwartet werden.

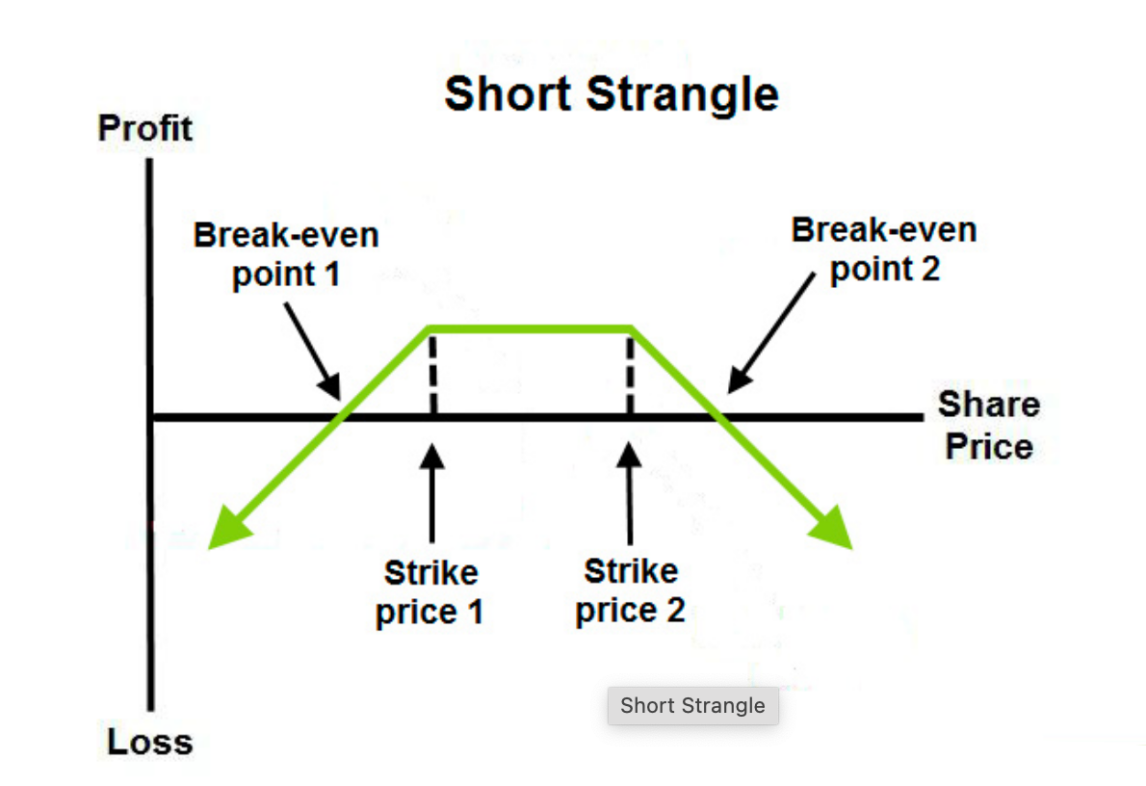
Ziel：

• Gewinn durch Vereinnahmen beider Optionsprämien, wobei bei unerwartet hoher Volatilität Verlustrisiken entstehen.
• Verbleibt der Kurs zwischen den beiden Ausübungspreisen, behält der Verkäufer die gesamte Prämieneinnahme.

Anwendungsbeispiel der Short-Strangle-Strategie

Angenommen, der BTC-Kurs steht bei $100,000 und Sie erwarten in den nächsten Tagen keine deutlichen Kursveränderungen. Daher wählen Sie die Short-Strangle-Strategie:

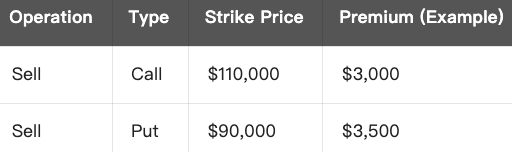
Gesamtertrag (Prämieneinnahme):

• Gesamtertrag = $3,000 (Call-Prämie) + $3,500 (Put-Prämie) = $6,500

Ergebnis bei Fälligkeit:

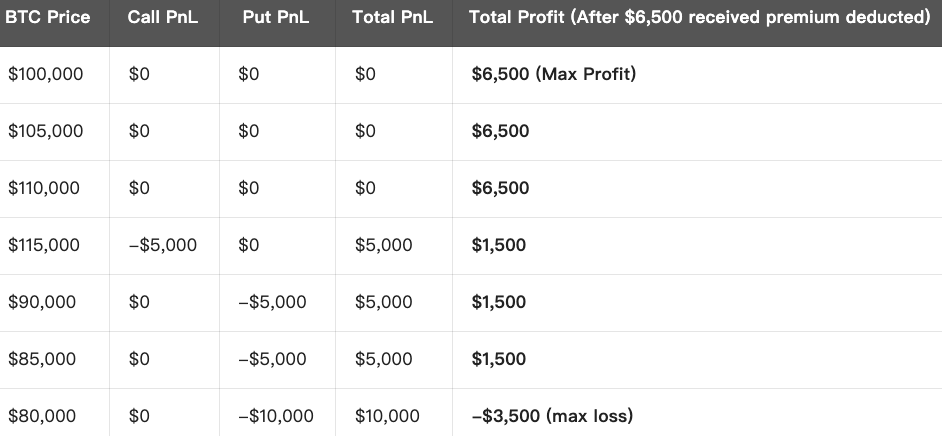
Strategie-Überblick:

Maximalgewinn: Liegt der Basiswert zwischen beiden Ausübungspreisen, entspricht die erhaltene Prämie dem Maximalgewinn ($6,500).

Maximalverlust: Bewegt sich der Marktpreis deutlich über die Ausübungspreise hinaus, wächst der Verlust theoretisch unbegrenzt. Der Maximalverlust beträgt die Differenz der Ausübungspreise ($110,000 - $90,000 = $20,000) abzüglich des Gesamtertrags ($6,500) = $13,500.

Break-Even-Punkte: Der Break-Even liegt an den Ausübungspreisen zuzüglich bzw. abzüglich des Gesamtertrags:

• Oberer Break-Even = $110,000 + $6,500 = $116,500
• Unterer Break-Even = $90,000 - $6,500 = $83,500

Anwendungsszenario:

• Die Short-Strangle-Strategie eignet sich für Seitwärtsmärkte, bei denen keine größeren Schwankungen erwartet werden, etwa wenn kommende Ereignisse (Finanzberichte, Konjunkturdaten) kaum Einfluss auf den Markt haben dürften.
• Das höchste Risiko besteht, wenn der Basiswert weit außerhalb der Ausübungspreise schließt.

Fazit:

Die Short-Strangle-Strategie ermöglicht das Vereinnahmen von Optionsprämien bei stabilen Marktbedingungen, birgt aber bei plötzlichen starken Kursbewegungen ein erhebliches Verlustrisiko.