Ризики, пов’язані з опціонами, та стратегії хеджування

Що таке хвостовий ризик

У фінансовій статистиці розподіли дохідності активів часто істотно відрізняються від ідеальної нормальної кривої. Замість цього спостерігаються так звані «важкохвості розподіли», у яких екстремальні події трапляються рідко, але у разі настання мають надзвичайно потужний і руйнівний ефект.

Для трейдерів опціонами:

• Стратегії продавця (наприклад, відкритий шорт пут, Iron Condor, Strangle) зазвичай приносять часті перемоги, проте у разі хвостових подій можуть спричинити катастрофічні збитки
• Стратегії покупця (наприклад, Long Put, Straddle) можуть захищати від хвостових ризиків або давати з них прибуток

Приклад:

Уявіть, що ви продали пут-опціон на BTC із страйковою ціною $80 000 (та отримали премію $1 000), коли поточна ціна активу становить $100 000. Ви впевнені, що BTC не впаде настільки різко.

Але якщо ринок обвалиться:

• BTC протягом кількох днів обвалюється до $60 000
• Ви зобов’язані купити один BTC за $80 000, коли його ринкова ціна — лише $60 000
• Збиток = $20 000 - $1 000 = $19 000

Очікувана вами невелика премія ($1 000) обертається величезним збитком, майже у 20 разів більшим — типовий вибух «хвостового ризику».

Форми хвостового ризику:

Як вирішувати й управляти хвостовим ризиком:

Висновок:

Хвостовий ризик — це надзвичайно руйнівна прихована небезпека для опціонних стратегій, особливо фатальна для тактик продавця. Не можна ігнорувати ризики лише через «високі шанси на виграш». Дійсно стійкі опціонні стратегії мають бути цілісною системою, здатною вистояти навіть в екстремальних ринкових умовах.

Що таке асимптотично оптимальна модель хеджування Whalley-Wilmott?

Модель Whalley-Wilmott, яку розробили Пол Вілмотт й Енн Воллі, є динамічною системою хеджування, що має на меті мінімізувати ризики хедж-витрат, особливо коли присутні транзакційні витрати. Ця схема належить до класу асимптотично оптимальних стратегій і ідеально підходить для портфелів із необхідністю частого коригування хеджу.

Основна концепція

В ідеальних умовах, згідно з моделлю Блека-Шоулза, продавець опціонів може повністю захеджувати ризики через постійний контроль дельти ("Continuous Delta Hedging"). Проте, у реальності:

• Транзакційні витрати (комісії, спред між купівлею й продажем) роблять часте перебалансування надто дорогим
• Дискретне (нерегулярне) хеджування не дає змоги повністю усунути ризик

Завдання моделі Whalley-Wilmott:

Знайти найкращий баланс між величиною торгових витрат і рівнем ризику: хеджувати частіше, ніж потрібно — дорого, рідше — ризиковано.

Ключова формула

Whalley-Wilmott визначає оптимальний інтервал хеджування ("No-Trade Region") — позицію коригують лише тоді, коли ціна базового активу виходить за межі цієї зони:

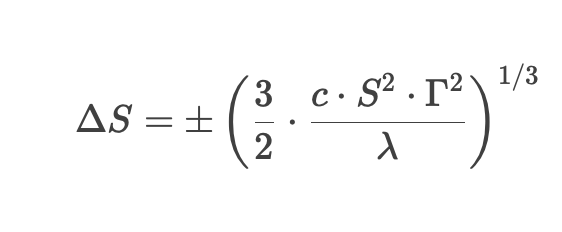
У цій формулі:

• Δ S — поріг зміни ціни, після якого потрібно хеджуватися
• c — трансакційні витрати (у відсотках)
• S — ціна базового активу
• Γ — гама опціону (друга похідна дельти за ціною активу)
• λ — коефіцієнт схильності до ризику

Правила стратегії:

1. Розрахуйте дельту для поточного опціону ("hedge ratio")
2. Встановіть допустимий інтервал ("No-Trade Region") — доки ціна активу знаходиться в цьому інтервалі, позицію не коригують
3. Якщо ціна виходить за межі зони, потрібно відкоригувати позицію так, щоб повернути дельту до цільового рівня
4. Особливості

5. Порівняння з іншими методами хеджування:

6. Підсумок

• Модель Whalley-Wilmott — це динамічна оптимізація процесу хеджування з урахуванням торгових витрат
• Зменшує надмірні перебалансування, контролює ризики через встановлення «зон без торгівлі»
• Ідеально підходить для опціонів із великою гамою або на ринках із високими витратами, є реалістичним удосконаленням моделі Блека-Шоулза

Ця модель широко застосовується в кількісних опціонних стратегіях та в управлінні ризиками, зокрема для інституційних інвесторів, яким потрібно ефективно балансувати витрати й ризики.